Consider classification problem as follows:
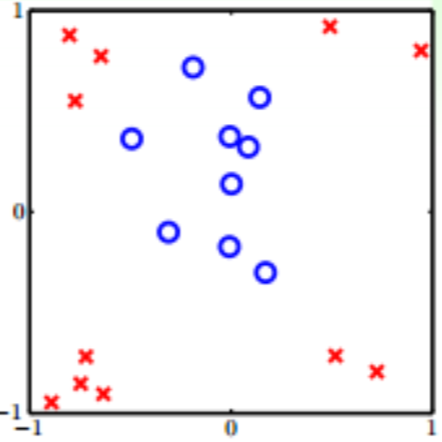
obviously, it is a nonlinear separable problem, but we can use a circle to reach our goal:
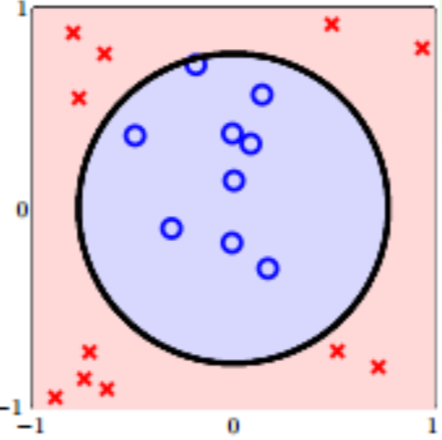
hypothesis of this model can be written as
\[h(\boldsymbol x)=\text{sign}(0.6-x_1^2-x_2^2) \tag{7.1}\]next we set $\boldsymbol z = (1,x_1^2,x_2^2)^{\text T}$ and $\tilde{\boldsymbol w}=(0.6,-1,-1)^{\text T}$, then rewrite $h$
\[h(\boldsymbol z)=\tilde{\boldsymbol w}^{\text T}\boldsymbol z \tag{7.2}\]In this transform, we map the point in space of $\boldsymbol x$ to space of $\boldsymbol z$, and these point is linear separable in the latter, we call this process Feature Transformation.
\[\boldsymbol x \in \mathcal X \mathop\longmapsto^{\boldsymbol\Phi} \boldsymbol z \in \mathcal Z \tag{7.3}\]In the problem above, $\boldsymbol z=\boldsymbol\Phi(\boldsymbol x)=(1,x_1^2,x_2^2)^{\text T}$.
Further, we have a general form of map function in quadratic hypotheses:
\[\boldsymbol\Phi_2(\boldsymbol x)=(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)^{\text T} \tag{7.4}\]From this formula we find that $\boldsymbol\Phi_1(\boldsymbol x)=(1,x_1,x_2)^{\text T}$ is a degenerate version of $\boldsymbol\Phi_2(\boldsymbol x)$, that means all components in $\boldsymbol\Phi_1$ is also included in $\boldsymbol\Phi_2$ and $\boldsymbol\Phi_2$ just adds the quadratic combination of $x_i$.
Then consider the general situation when sample vector $\boldsymbol x \in \mathbb R^{d+1}$ and feature dimension is $Q$, then we have
\[\boldsymbol\Phi_Q(\boldsymbol x) = (\boldsymbol\Phi_{Q-1}(x),x_1^Q,x_1^{Q-1}x_2,\cdots,x_d^Q) \tag{7.5}\]With feature transformation, we can use linear model to solve more problems that were previously difficult to slove. But it is important to note that when we do $Q$-th order polynomial transform where $Q$ is quite large, $\boldsymbol\Phi_Q(\boldsymbol x)$ here may be difficult to compute or store.
